можно оценить скорость света в одну сторону.
Введение.
В теме нет попытки изменить что-то в механике ТО. Решается просто небольшая задачка, с помощью которой попробуем очень грубо оценить некоторые величины.
Понятно, что синхронизация часов, предложенная Пуанкаре, а затем изменённая Эйнштейном содержит движение сигнала в две стороны Понятно, что в случае исследования скоростей сигналов применяемых в синхронизации, отличие в скоростях обнаружить невозможно из-за принятой синхронизации часов. Не будем пытаться определить скорости, но может их подскажут некоторые явления, которые, возможно, произошли из-за различия в скоростях. Можно попробовать на базе СТО ввести некоторое отличие в синхронизации часов и получить некоторое отличие от механики СТО. При этом интересно даст это какой-нибудь положительный результат или нет. При этом понятно, что если построить многообразие, то через рассмотрение метрики можно получить требуемые величины, то есть через ОТО. Но может существует более простой способ для рассмотрения некоторых процессов.
Единственная причина отличия скоростей сигналов может быть различие в способах измерения расстояния. То есть от наблюдателя - один способ, а к наблюдателю - другой способ, при этом каждый способ учитывает расстояние от наблюдателя. Раз будем применять одностороннюю синхронизацию, значит, будет зависимость в ИСО от расположения наблюдателя, так как даже для двух синхронизируемых точек положение наблюдателя будет влиять на синхронизацию часов в них. То есть выбирается точка наблюдения и относительно этой точки синхронизируются все часы.
Нас, конечно же интересует в первую очередь сигнал, который сообщает информацию из точки в точку. При этом нас интересует сигнал, который движется с максимальной скоростью в данной точке. Будем считать, что такую роль выполняет световой сигнал, пока не обнаружили сигнал более скоростной. Но так как мы считаем, что скорость сигнала не может быть постоянна и разная в разные стороны, то придётся это учитывать при синхронизации часов при изменении расстояния от наблюдателя.
Точки на одном расстоянии от точки наблюдения имеют эйнштейновскую синхронизацию, так как она получается испусканием из точки наблюдения сигнал во все синхронизируемые точки. Но точки расположенные на одной прямой проходящей через наблюдателя должны иметь другую синхронизацию, так как сигнал движется только в одну сторону. При этом надо помнить все ранее сказанные условия. Эта синхронизация может быть только выставление часов на НОЛЬ с приходом сигнала во все эти точки. То есть получим формулу:
, где за
– обозначим время в точке «А», в общем случае просто время t
– обозначим время в точке наблюдателя «О»
– обозначим скорость света из О в А
– обозначим скорость света из А в О
– обозначим скорость света в точке О.
– обозначим расстояние между О и А измеренное скоростью света c
Расстояние будем измерять скоростью c, так как расстояние в истинных скоростях мы определить не можем, так как эти скорости не известны.
Интересен пока только последний вариант синхронизации, так как эйнштейновская синхронизация задаёт механику СТО и известна.
Будем рассматривать только ось x, поэтому
Или отбросив индекс просто x, тогда
Надо учитывать, что x - это евклидова координата, которая откладывается одним отрезком. При этом понятно, что количество евклидовых координат в единице длины на определённом расстоянии от наблюдателя, не будет совпадать по количеству евклидовых координат в единице длины на другом расстоянии от наблюдателя.
Считаем скорость света неизменной в единицах длины, это даёт формулу в евклидовых координатах:
, где – некая функция, дающая изменение единицы длины.
Уравнение для интервала любой точки на оси x для бесконечно малого смещения будет:
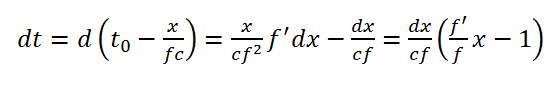
Бритва Оккамы даёт вариант:
или или
, примем , тогда
– не подходит, так как в точке 0 должно
Но может существует минимальное возможное расстояние от наблюдателя, тогда это расстояние и на этом расстоянии
То есть маленький вывод из данного расчёта: существует очень маленькая величина b, которая, определяет минимальное расстояние.
Теперь наш интервал выглядит: , а скорость света:
Интересует только оценка односторонней скорости, какая скорость больше, та, которая соответствует световому сигналу к наблюдателю или та, которая от наблюдателя?
Скорость на удаление увеличивает расстояние от наблюдателя, а скорость на приближение уменьшает.
Вывод.
Для любой рассматриваемой точки скорость удаления будет больше скорости на приближение, хоть и на ничтожно малую величину. Средняя скорость из скорости на удаление и на приближение будет равна c.
19.02.2016 Игорь Елкин
- Код ссылки на тему, для размещения на персональном сайте | Показать
