различие и ортогональность

Различны ли элементы множества {А, не-А}? Да, они различаются. Можно ли считать их противоположностями? Да, следует лишь указать «по отношению к чему» они таковыми являются. Можно ли трактовать А и не-А в качестве орт? Разумеется. В чем же тогда состоит отличие понятий противоположность и ортогональность? Для ответа на этот вопрос сравним более подробно эти понятия, обратившись к квантовой механике.

Если спин ориентирован вдоль оси Z, то прибор, если его поставить в этом же направлении, это покажет. Если же прибор развернуть в противоположном направлении, то показания прибора отобразят, что спин ориентирован обратно на 180 градусов.

Пока что ничего необычного. Все как обычно. Направления «+Z», «-Z» противоположны.

Если же прибор развернуть под 90 градусов по отношению к направлению Z, то новое измерение дает 50-процентную вероятность [2, с. 25] ориентирования спина к «+X» и такую же вероятность к «-Х». Направления «+X» и «-Х», естественно, противоположны, как и противоположны направления «+Z» и «-Z». Можно ли сказать, что они {«+X», «-Х», «+Z», «-Z»} различны? Конечно.

Рис.1. 50-процентная вероятность.

Ортогональность в пространстве взаимно перпендикулярных направлений численно выражается тем, что их скалярное произведение равно нулю. В квантовой же механике требование быть ортогональным в пространстве выражается в том, что только среднее значение является нулевым, чего нельзя сказать по отношению к отдельным измерениям. Это проиллюстрировано на рис. 2 [2, с. 27]:

Рис.2. Детерминизм рушится.

В произвольном выбранном направлении, т. е. не под прямым углом, статистические результаты распределены со средним значением, равным косинуса угла [2, с. 28]:

Рис.3. Произвольно выбранное направление.

Обычно, эти направления записываются с использованием матриц. Так, направления вверх и вниз, соответственно, можно записать в виде двух кет векторов. Умножаются же не они, а кет-вектор на бра-вектор или, наоборот, бра-вектор на кет-вектор [2, с. 68]:

Рис.4. Пара кет-векторов.

Так, умножение бра-вектора на кет-вектор дает нулевое значение, т. е. оно указывает на то, что они ортогональны (смотри рис. 5): <d|u>=0, <A|B>=0. Этот вывод, что направления вверх и вниз, выраженные таким образом, ортогональны, явно сбивает с толку, поскольку привычнее считать направления вверх и вниз противоположными.

Рис.5. Умножение матриц.

Предположим теперь, что имеются два множества {красный круг, синий круг, зеленый круг | круг}, {синий квадрат, красный квадрат, зеленый квадрат | квадрат}. Являются ли понятия круга и квадрата по отношению друг к другу ортогональными? Да, являются. Можно привести множество примеров, в которых ортогональность понимается именно таким образом: А и не-А ортогональны, поскольку они различны. И только тогда, когда эти орты заданы, можно будет говорить о сонаправленности и противонарпавленности.

Рис.6. Множества и координаты.

Если задать в качестве орт круг и квадрат, то каждый элемент множества {синий квадрат, красный квадрат, зеленый квадрат | квадрат} будет являться квадратом и каждый элемент множества {красный круг, синий круг, зеленый круг | круг} будет являться кругом. Но эти же отношения элементов множества могут быть выражены количественно. Вообще, отношения чисел сводятся к отношениям меньше, больше. И каждое следующее большее число получается из того, что меньше, В этом смысле первый и третий элементы, например, множества квадратов будут противоположными по отношению ко второму элементу, который может быть как синим, так и зеленым или красным квадратом. Таким образом, понятие противоположности применимо и по отношению к понятиям меньше, больше. Впрочем, именно это имеется ввиду, когда рассматривается выше/ниже, вперед/назад, влево/вправо.

Рис.7. Функции, множества, числа и орты.

Но можно в качестве орт, как уже говорилось, взять элементы рассматриваемого множества {синий квадрат, красный квадрат, зеленый квадрат}. Тогда возможно, например, такое: {красный квадрат со стороной 5 см, красный квадрат со стороной 8 см | красный квадрат}, {синий квадрат со стороной 8 см, синий квадрат со стороной 2 см | синий квадрат}, {зеленый квадрат со стороной 7 см, зеленый квадрат со стороной 3 см | зеленый квадрат}.

А что можно сказать в отношении точки координат, для которой направления красный квадрат, зеленый квадрат, синий квадрат заданы как то же самое? Этой точкой будет точка нуля, в которой нет красного квадрата, нет синего квадрата, нет зеленого квадрата: красный квадрат = зеленый квадрат = синий квадрат. И такая логика работает! Работает, в чем может убедиться каждый, запустив программу ниже в любой UNIX- среде (смотри рис. 8) [1]:

Рис.8. Ноль и один.

Когда же мы считаем элементы множества, например, такого как {синий квадрат, красный квадрат, зеленый квадрат | квадрат}, то абстрагируемся от синего, красного, зеленого и учитываем (при счете), что эти квадраты только чем-то отличаются, не конкретизируя чем именно. Понятие «следующий» тогда будет заключаться в том, что оно заменяется на «различается с каждым предыдущим», что и продемонстрировано в коде следующей программы (смотри рис. 9).

Рис. 9. Отношение «различаться с каждым предыдущим».

Итак, различные элементы можно трактовать как ортогональные. Если же элементы не только различны, но и имеют еще что-то общее, то только тогда их можно считать. В этом случае к элементам такого множества применимо понятие противоположности, в частности, отношение больше/меньше. И понятием, для которого противоположности будут тем же самым, будет единственное понятие - ноль. Поэтому и только поэтому отношение больше/меньше или плюс/минус для нуля является тем же самым. Сказать, что ноль не имеет знака - все равно сказать, что знак плюс и минус для нуля одно и то же.

Добавлено спустя 1 день 8 часов 59 минут 30 секунд:
Различны ли элементы множества {А, не-А}? Да, они различаются. Можно ли считать их противоположностями? Да, следует лишь указать «по отношению к чему» они таковыми являются. Можно ли трактовать А и не-А в качестве орт? Разумеется. В чем же тогда состоит отличие понятий противоположность и ортогональность? Для ответа на этот вопрос сравним более подробно эти понятия, обратившись к квантовой механике.

Если спин ориентирован вдоль оси Z, то прибор, если его поставить в этом же направлении, это покажет. Если же прибор развернуть в противоположном направлении, то показания прибора отобразят, что спин ориентирован обратно на 180 градусов.

Пока что ничего необычного. Все как обычно. Направления «+Z», «-Z» противоположны.

Если же прибор развернуть под 90 градусов по отношению к направлению Z, то новое измерение дает 50-процентную вероятность [2, с. 25] ориентирования спина к «+X» и такую же вероятность к «-Х». Направления «+X» и «-Х», естественно, противоположны, как и противоположны направления «+Z» и «-Z». Можно ли сказать, что они {«+X», «-Х», «+Z», «-Z»} различны? Конечно.



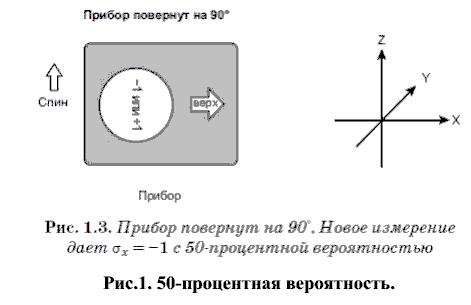
Ортогональность в пространстве взаимно перпендикулярных направлений численно выражается тем, что их скалярное произведение равно нулю. В квантовой же механике требование быть ортогональным в пространстве выражается в том, что только среднее значение является нулевым, чего нельзя сказать по отношению к отдельным измерениям. Это проиллюстрировано на рис. 2 [2, с. 27]:



В произвольном выбранном направлении, т. е. не под прямым углом, статистические результаты распределены со средним значением, равным косинуса угла [2, с. 28]:



Обычно, эти направления записываются с использованием матриц. Так, направления вверх и вниз, соответственно, можно записать в виде двух кет векторов. Умножаются же не они, а кет-вектор на бра-вектор или, наоборот, бра-вектор на кет-вектор [2, с. 68]:



Так, умножение бра-вектора на кет-вектор дает нулевое значение, т. е. оно указывает на то, что они ортогональны (смотри рис. 5): <d|u>=0, <A|B>=0. Этот вывод, что направления вверх и вниз, выраженные таким образом, ортогональны, явно сбивает с толку, поскольку привычнее считать направления вверх и вниз противоположными.



Предположим теперь, что имеются два множества {красный круг, синий круг, зеленый круг | круг}, {синий квадрат, красный квадрат, зеленый квадрат | квадрат}. Являются ли понятия круга и квадрата по отношению друг к другу ортогональными? Да, являются. Можно привести множество примеров, в которых ортогональность понимается именно таким образом: А и не-А ортогональны, поскольку они различны. И только тогда, когда эти орты заданы, можно будет говорить о сонаправленности и противонарпавленности.



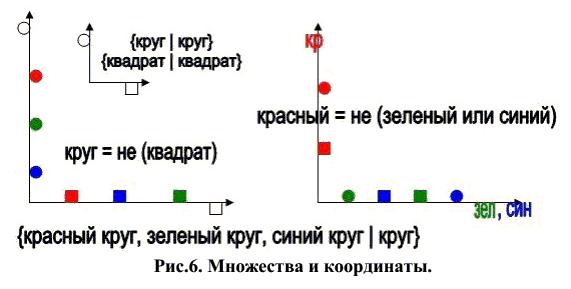
Если задать в качестве орт круг и квадрат, то каждый элемент множества {синий квадрат, красный квадрат, зеленый квадрат | квадрат} будет являться квадратом и каждый элемент множества {красный круг, синий круг, зеленый круг | круг} будет являться кругом. Но эти же отношения элементов множества могут быть выражены количественно. Вообще, отношения чисел сводятся к отношениям меньше, больше. И каждое следующее большее число получается из того, что меньше, В этом смысле первый и третий элементы, например, множества квадратов будут противоположными по отношению ко второму элементу, который может быть как синим, так и зеленым или красным квадратом. Таким образом, понятие противоположности применимо и по отношению к понятиям меньше, больше. Впрочем, именно это имеется ввиду, когда рассматривается выше/ниже, вперед/назад, влево/вправо.



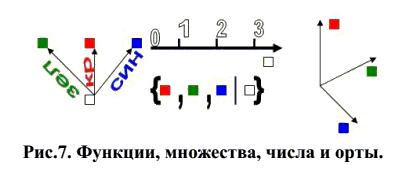
Но можно в качестве орт, как уже говорилось, взять элементы рассматриваемого множества {синий квадрат, красный квадрат, зеленый квадрат}. Тогда возможно, например, такое: {красный квадрат со стороной 5 см, красный квадрат со стороной 8 см | красный квадрат}, {синий квадрат со стороной 8 см, синий квадрат со стороной 2 см | синий квадрат}, {зеленый квадрат со стороной 7 см, зеленый квадрат со стороной 3 см | зеленый квадрат}.

А что можно сказать в отношении точки координат, для которой направления красный квадрат, зеленый квадрат, синий квадрат заданы как то же самое? Этой точкой будет точка нуля, в которой нет красного квадрата, нет синего квадрата, нет зеленого квадрата: красный квадрат = зеленый квадрат = синий квадрат. И такая логика работает! Работает, в чем может убедиться каждый, запустив программу ниже в любой UNIX- среде (смотри рис. 8) [1]:



Когда же мы считаем элементы множества, например, такого как {синий квадрат, красный квадрат, зеленый квадрат | квадрат}, то абстрагируемся от синего, красного, зеленого и учитываем (при счете), что эти квадраты только чем-то отличаются, не конкретизируя чем именно. Понятие «следующий» тогда будет заключаться в том, что оно заменяется на «различается с каждым предыдущим», что и продемонстрировано в коде следующей программы (смотри рис. 9).



Итак, различные элементы можно трактовать как ортогональные. Если же элементы не только различны, но и имеют еще что-то общее, то только тогда их можно считать. В этом случае к элементам такого множества применимо понятие противоположности, в частности, отношение больше/меньше. И понятием, для которого противоположности будут тем же самым, будет единственное понятие - ноль. Поэтому и только поэтому отношение больше/меньше или плюс/минус для нуля является тем же самым. Сказать, что ноль не имеет знака - все равно сказать, что знак плюс и минус для нуля одно и то же.

Добавлено спустя 1 день 9 часов 5 минут 43 секунды:
Литература
1) Булыгин В.В, Размышления о математике
2) Фридман Л. Квантовая механика. Теоретический минимум

Код ссылки на тему, для размещения на персональном сайте | Показать

Код: выделить все

<div style="text-align:center;">Обсудить теорию <a href="http://www.newtheory.ru/mathematics/razlichie-i-ortogonalnost-t3865.html">различие и ортогональность</a> Вы можете на форуме "Новая Теория".</div>


За это сообщение автора bulygin69 поблагодарил:

alexandrovod (25 апр 2017, 13:56)

bulygin69 писал(а): Можно ли трактовать А и не-А в качестве орт? Разумеется

Разумеется нет! Операцич "не-" применима только к утверждениям, поэтому следует понимать, что множество к которому принадлежат А и не-А есть множество утверждений. но чтобы можно было какой либо из элементов этого множества выбрать в качестве орта, оно должно быть представлять собой метрическое пространство, т.е. для любых двух его элементов А и В должнот быть определено скалярное произведение (А,В). Интересно, как вы определите скалярное произведение двух утверждений?

bulygin69 писал(а):Различны ли элементы множества {А, не-А}? Да, они различаются. Можно ли считать их противоположностями? Да,...

Тема интересная и емкая, но я попытаюсь раскрыть ее по-другому. Заметьте, это не дискредитация Вашего подхода, и даже не его критика, а ее рассмотрение на основании общего понятия «отношение», которое, так или иначе, присутствует в Вашем комментарии. При этом замечу еще следующее. Всякое исследование, как это уже давно признано, начинается с возникновения проблемы, т. е. с констатации той трудности, с которой мы встречаемся при объяснении фактов или результатов каких-то исследований. Древнегреческое слово «проблема» означает «трудность, или препятствие», но не противоречие. Однако в применении к современному научному знанию проблему трактуют именно как противоречие между старыми парадигмами и новыми принципами. Отсюда возникает представление, что любой процесс познания – это борьба нового со старым (до полной победы нового над старым, по Марксу) или в более мягкой версии (по Лакатосу, например) – противоречие между теориями приводит к смене научных парадигм.

В историческом развитии научного познания ясно выявляются два различных подхода к процессу исследования, отображающих установление исходного его пункта. Если эмпирики к такому началу следуют индуктивным путем (исследование как можно большего числа фактов, их анализ и обобщение), то теоретики всегда исходят из некоторой исходной гипотезы, из которой они затем дедуктивно выводят различные следствия, и, если удастся, тестируют их на практическую осуществимость. Эти два пути нельзя рассматривать отдельно, а, тем более, противопоставлять их. В сложном научном процессе индукция и дедукция, как правило, следуют в одной упряжке, поддерживая друг друга. Но здесь должно быть ясно одно: индукция должна быть полной, а дедукция – логически корректной, из чего немедленно следует, что индуктивным путем невозможно создать общие понятия, т. е. такие исходные начала знания, которые содержат в своем объеме бесконечное (или неперечислимое) число фактов. Все такие понятия, поэтому, вводятся в научное теоретическое знание с помощью различного рода описаний (дескрипций) и в своих теориях называются первичными или неопределяемыми. В математике – это «число», «множество», и, конечно, «отношение».

Так, мы не можем дедуктивно определить, что такое «отношение», потому что над ним нет более общего (родового) понятия. Например, мы определяем дедуктивно понятие «простое число» («это целые числа, которые делятся только на единицу и самое себя»), предполагая при этом, что родовое понятие «целое число» нам знакомо и понятно. Мы можем только пояснить, что отношение, во-первых, может устанавливаться, как минимум, между двумя предметами (бинарные отношения), которые при этом рассматриваются одновременно. Поскольку, предметов как минимум два, то они всегда различные, т. е. различие – это неотъемлемое свойство всякого бинарного отношения. Но, помимо различия, между предметами любого отношения должно быть и тождество = по одному или нескольким характеристическим признакам, т. е. то или иное отношение, которое можно охарактеризовать как единство тождества и различия, существует только между элементами одного множества.

Особой формой отношения является отношение абсолютного тождества, или рефлексивность: А = А (каждый объект тождествен только себе и никакому другому). Многие математики путают отношение тождества с отношением равенства: a = b, где a и b – тождественные свойства объектов А и В. Например, длина двух бревен или скорость двух ТС.

В математике имеют дело с конкретными отношениями – «меньше»/«больше», «равно», «конгруэнтно» и т. д. Особое значение имеет отношение эквивалентности, которое рефлексивно, симметрично и транзитивно; отношении эквивалентности находятся все элементы, образующие конкретное множество (или подмножество некоторого множества).

Что есть отношение противоположностей? Или иначе: чему эквивалентно отношение противоположностей? Мой ответ: оно равно нулю. Именно поэтому любое общее понятие, которое представляет собой единство противоположностей, с позиции формальной логики неразрешимо противоречиво, или парадоксально, если его рассматривать как конкретное отношение. Так, сумма всех целых чисел – положительных и отрицательных - равна 0, как равна нулю и любая их антисимметричная пара: 2 и – 2, например. Поэтому и сумма противоположностей любого общего отношения также можно оценить эквивалентностью нулю. В разговорном языке такого рода общие отношения оцениваются антонимами (парами слов, имеющими противоположные значения): любовь-ненависть, дружба-вражда, добро-зло и пр. Противоположности, таким образом, это предельный случай отношения, поскольку они также имеют инвариант (например, единицу для целых чисел), но их различие носит, я бы сказал, радикально-непримиримый характер. В логике суждений, например, в такой оппозиции выступают утвердительное суждение и его отрицание, что приводит к «стиранию» первичной мысли, и утверждения на место следующей.

bulygin69 писал(а):В чем же тогда состоит отличие понятий противоположность и ортогональность?

Ортогональности, как я понимаю, это отношение общих понятий, которое имеет единственную общую точку, также обозначаемую нулем. Эта точка во всех геометрических (координатных) отображениях выступает в качестве начала координат. Отличие противоположности и ортогональности - в размерности: каждое единство противоположностей – одномерно (одна координатная ось, распространяющаяся в бесконечность влево и вправо), а каждое единство общих понятий – многомерно. Хотя, я думаю, эта многомерность не превышает число 3. Но это уже другая тема.

Валентин Попов писал(а):Ортогональности, как я понимаю, это отношение общих понятий, которое имеет единственную общую точку, также обозначаемую нулем.

По моему мнению ортогональность несколько другое, хотя и близкое к вашему. Если множество связанных элементов одного подпространства проектируются на другое подпространство единым объектом по модулю не больше нуля, то эти подпространства взаимно ортогональны, а если проекция больше нуля то они как минимум по одной координате противоположны.
С уважением Овод

che писал(а):Можно ли трактовать А и не-А в качестве орт?
...
Разумеется нет! Операцич "не-" применима только к утверждениям, поэтому следует понимать, что множество к которому принадлежат А и не-А есть множество утверждений. но чтобы можно было какой либо из элементов этого множества выбрать в качестве орта, оно должно быть представлять собой метрическое пространство, т.е. для любых двух его элементов А и В должнот быть определено скалярное произведение (А,В). Интересно, как вы определите скалярное произведение двух утверждений?

Вам привести множество примеров с системой координат с ортами X и Y? ... Так и определяется, что скалярное произведение X на Y дает ноль.

bulygin69 писал(а):Вам привести множество примеров с системой координат с ортами X и Y?

Не надо! Понятие ортогональности функционирует во множествах, являющихся линейными пространстваеми, и примеров таковых я знаю наверняка больше чем Вы. Например понятие ортогональности может бвть применено к функциям, если в качетве скалярного произведения принять, например, такое выражение:


Речь же шла о том, что множество высказываниий, как предикатов логических выражений, допускающих операцию "не-", не является метрическим пространством, пока в нём разумным образом не определено скалярное проиведение. Вот я и предлагал Вам придумать такое определение, прежде чем рассуждать об ортогональности высказываний

Валентин Попов писал(а):В чем же тогда состоит отличие понятий противоположность и ортогональность?
...
Ортогональности, как я понимаю, это отношение общих понятий, которое имеет единственную общую точку, также обозначаемую нулем. Эта точка во всех геометрических (координатных) отображениях выступает в качестве начала координат. Отличие противоположности и ортогональности - в размерности: каждое единство противоположностей – одномерно (одна координатная ось, распространяющаяся в бесконечность влево и вправо), а каждое единство общих понятий – многомерно. Хотя, я думаю, эта многомерность не превышает число 3. Но это уже другая тема.

В статье показано, что то, что различно, можно трактовать и как то, что противоположно и как то, что ортогонально. ... Например, красный_квадрат и зеленый_квадрат можно взять в качестве орт. Но эти же элементы множества (множества квадратов) можно трактовать и как противоположности. Противоположные по отношению к чему? По отношению к (красный_квадрат=зеленый_квадрат), т.е. красный_квадрат противоположен зеленому_квадрату по отношению к (красный_квадрат=зеленый_квадрат).

bulygin69 писал(а):то, что различно, можно трактовать и как то, что противоположно и как то, что ортогонально.

Можно! Трактуйте -- Вам за это ничего не будет!
Но и толку от такой трактовки... до звезды пришей рукав

che писал(а):Вам привести множество примеров с системой координат с ортами X и Y?
...
Не надо! Понятие ортогональности функционирует во множествах, являющихся линейными пространстваеми, и примеров таковых я знаю наверняка больше чем Вы. Например понятие ортогональности может бвть применено к функциям, если в качетве скалярного произведения принять, например, такое выражение:

Речь же шла о том, что множество высказываниий, как предикатов логических выражений, допускающих операцию "не-", не является метрическим пространством, пока в нём разумным образом не определено скалярное проиведение. Вот я и предлагал Вам придумать такое определение, прежде чем рассуждать об ортогональности высказываний

Надо! Еще как надо! Вы, видимо, не скажите, что S и t в записи S=v*t ортогональны? Орта расстояния и орта времени не ортогональны? Можно, конечно, определить ортогональность как то, что подчиняется правилу произведения модулей на косинус угла. Только вот беда - сразу возникают вопросы а что есть угол, что есть косинус, что есть произведение. Здесь телега впереди лошади.

Добавлено спустя 15 минут 4 секунды:

che писал(а):Можно! Трактуйте -- Вам за это ничего не будет!
Но и толку от такой трактовки... до звезды пришей рукав

А вы думаете, что многим не по себе от того, что вы что-то не понимаете? Работающей программе, которая функционирует, используя, в частности, такое толкование противоположности и ортогональности, нет до этого никого дела, уж поверьте.

bulygin69 писал(а):Например, красный_квадрат и зеленый_квадрат можно взять в качестве орт. Но эти же элементы множества (множества квадратов) можно трактовать и как противоположности.

В качестве координат могут выступать только независимые общие понятия, отображаемые графически числовыми множествами. Наглядный пример – декартова система координат, где каждая ось может отображать любое независимое физическое понятие: пространство, время или импульс. Тогда, задав масштаб этого понятия (его физическую меру), каждая точка таких координатных осей будет отображать определенное численное значение данной физической величины. «Красный квадрат» и «зеленый квадрат» - элементы одного и того же понятия, которое можно назвать, допустим, «цветные квадраты». Отсюда сразу видно, что все «цветные квадраты» различны как элементы данного конкретного множества, но они не противоположны и не ортогональны. Наглядно (графически) они лежат на одной оси.

bulygin69 писал(а):Работающей программе, которая функционирует, используя, в частности, такое толкование противоположности и ортогональности, нет до этого никого дела,

У Вас какое-то религиозное отношение к "работающей программе". Основа любой программы – алгоритм, записанный на машинном языке (с помощью нулей и единиц). Именно поэтому вычислительная машина не в состоянии реагировать на тонкости и логические уловки человеческого языка. Люди в разговоре (даже вполне научном) сопровождают свои слова жестами или мимикой, используют метафоры, гиперболы, сарказм, недомолвки и много других речевых и неречевых средств, которые позволяют им говорить как будто нечто определенное, а на самом деле подразумевать нечто другое или не подразумевать ничего (просто, как сказал Н. Бор, «злоупотреблять языком»). В то же время компьютер не может обрабатывать какие бы то ни было команды до тех пор, пока они не переведены в нули и единицы и не загружены в его твердотельную электронную начинку.

Писать программы в машинном коде – занятие крайне утомительное (так поступали на заре компьютерной эры). Дело значительно упрощается, если использовать языки программирования, ориентированные на решение определенного класса задач. Теоретически для решения большинства задач можно использовать любой язык программирования, но на практике оказывается, что написать программу для конкретной задачи проще на одном языке, чем на других. Как Вам должно быть известно, каждый язык программирования имеет свой собственный ключевой набор, состоящий из слов, букв, чисел или специальных символов. Некоторые ключевые слова выполняют функцию глаголов, другие – существительных, третьи – логических операций и т. д. Они связываются друг с другом в соответствии с синтаксическими правилами, которые есть не что иное, как правила формальной логики, образуя предложения языка программирования. Задача программиста состоит не в том, чтобы самому решить задачу, а в том, чтобы создать такую последовательность команд (алгоритм), которая позволит компьютеру отыскать решение самостоятельно и гораздо быстрее, чем если бы это делал человек.

Быстрое выполнение вычислений – это работа, предназначенная для компьютера, а вот содержательная часть работы, связанная с разработкой пошагового алгоритма, который указывает компьютеру, каким образом и в какой последовательности тот должен выполнять задание, поручают человеку с его интеллектом, наделенным не только алгоритмической, но обобщающей и абстрагирующей функциями. Именно последние функция способны выводить разум из логических тупиков, создаваемых философствующим математиками, не понимающими, где формальная логика утрачивает свой когнитивный ресурс.